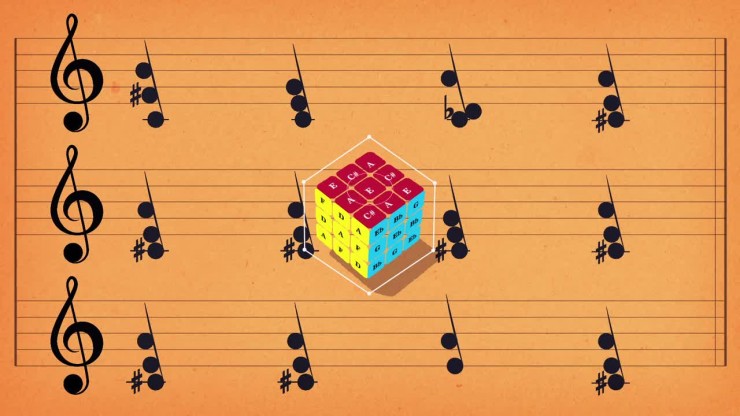
Which do you think is more difficult - playing the piano, or solving the Rubik’s Cube?
Your answer will of course depend on which you think yourself more familiar with. However, if you are well-acquainted with either, it might surprise you to know that you already have a key to understanding the other as well, as accomplished mathematician, composer and musician Michael Staff recently explained.
In 1974, the world’s best-selling toy was created - the deceptively simple-looking Rubik’s Cube. The classic version of this three-dimensional combination puzzle features a cube with an internal pivot mechanism that allows each of the six faces to turn independently. Each face consists of nine segments, with six possible colours for each segment, so turning the faces mixes up the colours. The puzzle is considered solved when each face is returned to having only one colour.
Named after its inventor, a young professor of architecture named Erno Rubik, the cube was first used as a model for Erno to explain spatial relationships to his students.
Michael Staff took it one step further, drawing an intriguing parallel between Rubik’s Cube with piano chord progressions through an area of mathematics called group theory.
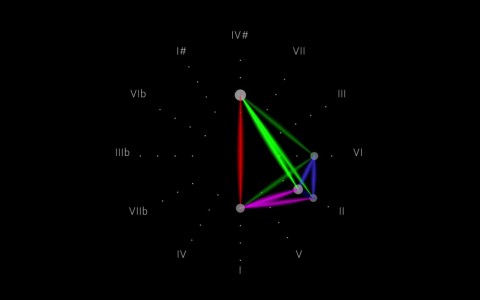
As illustrated by the above video, there are four basic rules (also known as axioms, in mathematics) that apply to both the Rubik’s cube as well as to musical notes. They are namely:
- Closure: There are a fixed number of elements, and they can be rearranged without affecting their values. (The number of segments and configurations in a Rubik’s Cube puzzle is always the same.)
- Associative: The elements can be used to perform an action, in any order. (The configuration will remain the same regardless of whether I rotate the face of a Rubik’s Cube clockwise once, then twice, or clockwise twice, then once.)
- Identity: A common ‘identity’ element must exist, to which elements will remain unchanged when added to it. (In terms of the Rubik’s Cube, this identity is not turning it at all.)
- Inverse: Two of the elements within the group must be inverse, which will result in the ‘identity’ element when they are brought together. (Turning any face of the Rubik’s Cube once to the right, and once to the left, will bring it back to its original configuration.)
These four basic properties of mathematics make up the group theory system, and both solving the Rubik’s Cube and playing the piano relies on these same properties.
In mathematics, a group is a particular collection of elements. When playing the piano, we have only twelve unique notes - a collection of twelve elements, in other words.
By checking the abovementioned rules, we can verify that the keys of a piano form a group. So, since an element can be applied to any coloured square in the Rubik’s cube, it can also apply to any note on the piano.
The process developed by Michael Staff to use these basic principles to combine music with the Rubik’s cube involves mapping notes to each segment on the cube. A chord can also be seen as a group of the notes making it up, and thus a subgroup of all piano notes. Subgroups follow the same rules that the groups follow. Each face of the Rubik’s Cube is assigned to one chord, and each row and column on a face is a different chord position.
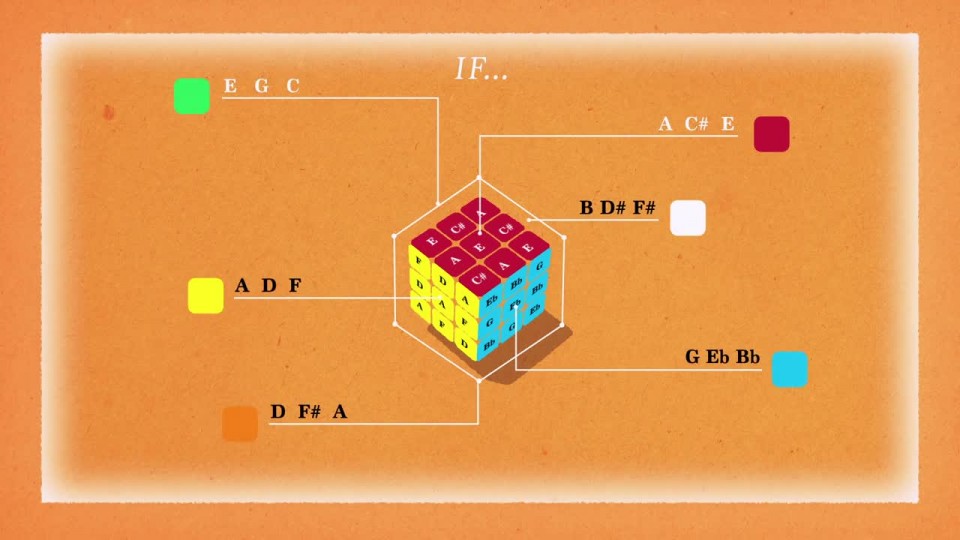
Therefore, with every square on the Rubik’s Cube thus mapped to a note within a chord, once you have ensured that your chords are harmonious, you would have also solved the Rubik’s Cube!
This abstract application of music to the Rubik’s Cube amply demonstrates how playing the piano is not just about entertainment - it enhances your appreciation and deepens your understanding of logic, patterns, and even mathematics. Once you grasp the concepts that Michael Staff exhibited on this novel relationship, you’ll see that it doesn’t matter if playing the piano or solving the Rubik’s Cube is more difficult – you can do both!